匈牙利算法总结

Part 0：前言

学了这个算法好多次了，是时候总结一下啦😆

Part 1：几个概念

• 二分图：一类特殊的图，它可以被划分为两个部分，每个部分内的点互不相连。
• 最大匹配数：二分图中没有公共端点的边的数量的最大值。
• 最小点覆盖：我们想找到最少的一些点，使二分图所有的边都至少有一个端点在这些点之中。倒过来说就是，删除包含这些点的边，可以删掉所有边。
• 匈牙利算法：一种用来解决最大匹配数和最小点覆盖问题的算法。

Part 2：二分图最大匹配问题

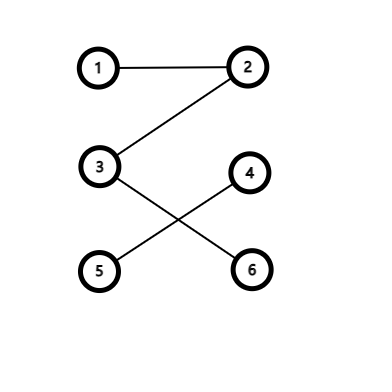
这里举例一个二分图，来模拟匹配的过程。

很明显，这里的最大匹配是3。

匈牙利算法的过程模拟：

我们先暂时把1和2连在一起。

现在3也可以和2连，这时我们返过去看和2相连的1。

由于1只能和2连，所以3连不上2。

那么3还有选择么？有，可以和6连。

这时6只能和3连。

再看4，和5连即可。

这就是匈牙利算法的流程，至于具体实现，我们来看看代码：

int M, N;            //M, N分别表示左、右侧集合的元素数量
int Map[MAXM][MAXN]; //邻接矩阵存图
int p[MAXN];         //记录当前右侧元素所对应的左侧元素
bool vis[MAXN];      //记录右侧元素是否已被访问过
bool match(int i){
    for (int j = 1; j <= N; ++j)
        if (Map[i][j] && !vis[j]){ //有边且未访问
            vis[j] = true;                 //记录状态为访问过
            if (p[j] == 0 || match(p[j])){ //如果暂无匹配，或者原来匹配的左侧元素可以找到新的匹配
                p[j] = i;    //当前左侧元素成为当前右侧元素的新匹配
                return true; //返回匹配成功
            }
        }
    return false; //循环结束，仍未找到匹配，返回匹配失败
}
int Hungarian(){
    int cnt = 0;
    for (int i = 1; i <= M; ++i){
        memset(vis, 0, sizeof(vis)); //重置vis数组
        if (match(i))
            cnt++;
    }
    return cnt;
}

通过算法我们可以发现，单次找边的过程是 $O(m)$ 的，一共有 $n$ 个点，所以总体复杂度为 $O(nm)$。

（因为复杂度大，所以题目的限制一般较大，可以直接用邻接矩阵存储）

Part 3：二分图最小点覆盖问题

这里引入König定理：

一个二分图中的最大匹配数等于这个图中的最小点覆盖数。

直接解决。

Part 4：例题

这里只举例一题：洛谷 P1129 [ZJOI2007] 矩阵游戏

小 Q 是一个非常聪明的孩子，除了国际象棋，他还很喜欢玩一个电脑益智游戏――矩阵游戏。矩阵游戏在一个 $n \times n$ 黑白方阵进行（如同国际象棋一般，只是颜色是随意的）。每次可以对该矩阵进行两种操作：
行交换操作：选择矩阵的任意两行，交换这两行（即交换对应格子的颜色）。
列交换操作：选择矩阵的任意两列，交换这两列（即交换对应格子的颜色）。
游戏的目标，即通过若干次操作，使得方阵的主对角线(左上角到右下角的连线)上的格子均为黑色。
对于某些关卡，小 Q 百思不得其解，以致他开始怀疑这些关卡是不是根本就是无解的！于是小 Q 决定写一个程序来判断这些关卡是否有解。

通过枚举样例，我们发现：任意2个黑色方块，如果它们初始状态时不在同一行（列），那么无论如何交换，它们都不会在同一行（列）。

所以我们只需判断每一行是否都可以合法匹配即可。

AC代码：

#include<bits/stdc++.h>
using namespace std;
int mp[205][205],p[205],vis[205],n,T;
bool match(int i){
	for(int j=1;j<=n;j++) {
		if(mp[i][j]&&!vis[j]){
			vis[j]=1;
			if(!p[j]||match(p[j])) {
				p[j]=i;
				return 1;
			}
		}
	}
	return 0;
}
int Hungarian(){
	int cnt=0;
	for (int i=1;i<=n;i++) {
		memset(vis,0,sizeof(vis));
		if (match(i))cnt++;
	}
	return cnt;
}
int main() {
	scanf("%d",&T);
	while(T--){
		scanf("%d",&n);
		memset(p,0,sizeof(p));
		for(int i=1;i<=n;i++)
			for(int j=1;j<=n;j++)
				scanf("%d",&mp[i][j]);
		if(Hungarian()==n)puts("Yes");
		else puts("No");
	}
	return 0;
}

Part 5：总结

匈牙利算法是一个比较基础的图论算法，思路较简单，一定要记牢啊😙